Hi! It's been awhile. I lost motivation for a while there, and moved to a different state, but I won't keep boring you with all that. Suffice it to say that hopefully I will start posting more regularly now as I head into my PhD!
Now, this post will be about what I learned and created this summer during my internship at Stottler Henke (SHAI). In general, I don't plan on discussing such (gasp) real-world applicable things as much going forward on this blog, in case anyone was concerned.
Problem Setup
Now, let's talk about plagiarism. Here's the setup: we have a (very) large corpus (say, Wikipedia) of $N$ "sensitive" or "source" documents, which may or may not have been plagiarized by our query document. When we say plagiarism, we don't necessarily mean the whole document -- it could just be that a key sentence was copied, or a paragraph with crucial information was summarized at some (potentially random) point within the query document. Now, for exact matches, this is a relatively straightforward task, although it takes some clever data structures that I won't discuss in this post to get the runtime to depend only (linearly) on the length $m$ of the query document rather than $N$ (all the source documents we have to search through). This is what had already been accomplished when I arrived for my internship, and my task was to see what might be possible when our job was not just to find exact matches, but also "fuzzy" matches. After all, a smart plagiarizer would try and hide their illicit behavior. But what does "fuzzy" even mean? So glad you asked, and if you have a good definition please send it my way.
Nevertheless, onwards. It seemed as good a starting place as any was the PAN Conference, a conference whose central theme in 2011-2015 was plagiarism detection! Now, this seemed to be more of a competition and less of a thoroughly peer-reviewed venue, but nonetheless there were some interesting ideas floating around there, in case you want to see other things outside of what I will talk about in this post. In addition, they had a nice (albeit small) dataset and evaluation framework (which were a bit difficult to find but not impossible) that allows for an objective scoring and evaluation of any algorithm one might come up with! Beyond the dataset (and floating ideas), and perhaps most importantly, they also had a very nice framework for plagiarism detection, which I will now describe.
The framework they describe splits plagiarism detection into two main tasks:
- Source Retrieval: This refers to the task of (efficiently) narrowing our search down from $N$ (which is just overwhelmingly large) possible source documents to just $k$ (which we think of as some reasonable constant). We will do a more detailed plagiarism detection analysis on these $k$ documents in the next phase. You can think about source retrieval as a sort of google search where the query document is typed into Google and the source documents as the possible "websites". Of course, like anyone ever, we only have time to look at the first page (a.k.a. the first $k$ source documents) results that Google spits out.
- Text Alignment: This refers to the task of, well, actually "finding" the instances of plagiarism between the query document and the top $k$ source documents. This is where the fun really begins!
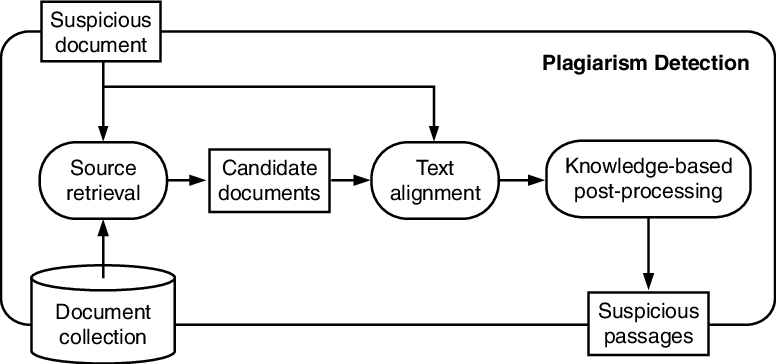
In this post we will discuss some general strategies for source retrieval, but all of them involve some sort of "search engine" such as ElasticSearch or Lucene or maybe Google has an API (I dunno just pick your favorite one), and go a bit more into depth on some ideas I had for the text alignment phase.
Source Retrieval
I think some discussion of the source retrieval step is warranted here, but I will try and keep this section brief and focus more on the algorithms I think are interesting for the text alignment phase.
Basically, we just need to figure out how to input/give our query document to whatever search engine we are using. The search engine I was tasked with using had a finite limit on how many words the query could be, which is part of what makes things slightly tricky about this. Let's talk about some possible solutions:
- If our document is very long, we can narrow it down to the top $w$ keywords (for your choice of $w$) in a fairly straightforward manner, depending on the search engine you are using or how you are indexing the source documents. Basically, the idea is to get the TF-IDF scores of each word in they query document, and make a new query that's just based on the top $w$ words according to this score. What is TF-IDF? So glad you asked. TF stands for term frequency, which is just the number of times the term appears in the query document. IDF, which stands for inverse document frequency, requires data from the indexed source documents, and it is equal to $$\log \left ( \frac{n+1}{m+1}+1\right) $$ where $n =$ number of source documents and $m=$ how many (source) documents the term appears in. If your index (again, Lucene, etc.) gives you quick access to $m$ and $n$ then you are good to go! Note that in this setup, rare words (w.r.t. the overall corpus) are rewarded much more highly than words (such as "the" or "he") that appear in almost every document. Also note that this method doesn't take into account the ordering of the words in the query document.
-
The previous method is fairly fast, and only requires one use of the search engine after you have created your new query. However, imagine that someone has hidden a small plagiarized passage about a violin within a very long article (which hasn't been plagiarized) about football. It is overwhelmingly likely that the violin words are "drowned out" by all the football, and the above method won't work. Now this is a particularly difficult kind of plagiarism to detect, but what good would our tool be if we just gave up on the tough examples? Plus, people usually try to hide their plagiarism.
The next idea is an attempt to address this. It is simple: just split the query document into small enough chunks (of desired length), and treat each as a separate query to your search engine/index. This is much more likely to catch the nefarious example I described above, but has the drawback of being much slower and scaling with the length of the query document. One must also decide how to decide which results to prioritize between the chunks. You could take the ones with the highest overall scores (according to your search engine), but that may ignore some chunks altogether. You could also take the top few results from each chunk, but if your query is very long this could get very expensive later in the text alignment phase (in which we have to do detailed analysis on every document retrieved in this stage).
Text Alignment
Ok, now we can talk about more fun stuff! Or at least, stuff we have a bit more control over. A small note: I think it makes a lot of sense to do all matching on a word-by-word basis (rather than character-by-character) if we are looking to detect obfuscated plagiarism. Why I think this will become even more clear when we discuss Smith-Waterman score functions, but this also makes sense because we can then take out punctuations, whitespaces, and "stopwords" (pronouns, prepositions, etc.), and reduce our document to something much simpler.Greedy Tiling
I am basically going to briefly summarize what I think are the important takeaways from this paper by Wise. It's going to be brief, and I mean it this time. The setup is that we have some source document, and some query document, and we want to find exact matches between them efficiently.
The idea is super simple: just take the longest exact match first, "tile" it (meaning mark it so that no matches touch that area in the source or query document again), and repeat until there are no more matches of at least the minimum match length $t$. That's it. Some notes:
- Technically, the worst case runtime of the most basic form of the algorithm is $O(n^3)$, if $n$ is the length of both the query and source documents. Which is bad. However, with some tricks, we can improve the worst case runtime to $O(n^2)$ (still bad), but crucially, the average case runtime (empirically) is $O(n)$ (good!). The rough idea is as follows: create an inverted index of both the query and source document mapping each phrase of length $t$ to the indices it occurs at. I should note that this can be accomplished via a rolling hash function for a very speedy mapping process, but since I was using Python dictionaries I didn't bother with this. Then you just run through the query phrases, checking if any appear in the source dictionary, and if so expanding them if necessary. I am hiding some details, but this is the gist of it. TLDR: it's pretty much linear time.
- This algorithm is not technically optimal. Here, by "optimal", we mean that it doesn't necessarily maximally tile the query document. Here is a concrete example: consider $\mathbf{src} = b a a d c a a a a b a a$ and $\mathbf{query} = c a a b a a d $. Greedy tiling will find the match $a a b a a$ rather than the two matches $caa$ and $baad$. So, not technically optimal, but one could argue that we might want to find longer matches over shorter matches anyway. Also, this is a pretty pathological example.
Smith-Waterman
This is probably my favorite algorithm of the bunch. Here's a wikipedia article on it, if you're into that sort of thing, but I will do my best that you don't need to reference it. The original paper is also all of 1.5 pages long, a real banger if you ask me.
My one line description of this algorithm would be "The classic edit distance dynamic programming algorithm but with user-defined scoring". Since we're talking dynamic programming, we fill in an $m+1 \times n+1$ matrix $H$ of scores, where $m$ is the length of the query, and $n$ is the length of the source. We reward matching words, and penalize mismatching words and whenever we have to introduce a "gap", meaning skip over a word in the query or source document. $$H_{i,j} = \max \begin{cases} H_{i-1,j-1} + \mathbf{score}(query\_words[i], source\_words[j]) \\ H_{i-1,j} + \mathbf{gap\_penalty} \\ H_{i, j-1} + \mathbf{gap\_penalty}. \end{cases} $$ We then take matches by finding entries of the matrix above a certain score threshold $\beta$. Note that we do this on a word by word basis, as discussed above. Also note that the runtime is at least $O(mn)$, which is slow. I admit that when I initially saw this runtime, as a theoretician, I was like oh good it's polynomial! What a fast algorithm, this is perfect. Then I ran it on my laptop and realized why I usually stick to theory.
Next, I claim that this algorithm, like the edit distance algorithm, is optimal! But what does that even mean here? And what are reasonable score and gap_penalty functions?? Great questions. The answer to the first question is rather dumb: the algorithm is optimal for whatever score/gap penalty functions you choose, so you could choose some nonsense functions and your algorithm will output nonsense. At least it will be optimal nonsense, I suppose. So let's talk about reasonable scoring and gap penalty functions.
Smith-Waterman Scoring Functions
An example of a really simple (and canonical) score function could be as follows: $\mathbf{score}(w_1, w_2) = 1$ if $w_1 = w_2$, otherwise $\mathbf{score}(w_1, w_2) = -p$. Usually $p$ will be in the range of roughly $(0.05, 0.5)$. Taking $p$ too large doesn't allow for hardly any mismatches (aka "fuzziness"), while $p$ being too small will result in very fuzzy matches, to the point where a human would usually conclude that this is not a match. As for the gap penalty function, I think a good rule of thumb is to penalize gaps and misamtches the same, so $\mathbf{gap\_penalty} = -p$.
Now, I wasn't exactly satisfied with this score function, and so I had what I thought was a really cool idea. My idea was to use a (pretrained) word embedding as a score function to capture semantic similarities! $ \mathbf{score}(w_1, w_2) = $ $$ \begin{cases} -p & \text{ if } \mathsf{cs}(E(w_1), E(w_2)) < \alpha \quad \text{(mismatch)}\\ 2\cdot (\mathsf{cs}(E(w_1), E(w_2)) -\alpha) & \text{ if } \mathsf{cs}(E(w_1), E(w_2)) \geq \alpha. \quad \text{(match)} \end{cases} $$ where $\mathsf{cs}$ is the cosine similarity, and $E$ is the pretrained word embedding. For concreteness, just consider $\alpha = 0.5$. What this score function does is it sees for example $w_1 = amazing$ and $w_2 = incredible$, then it may not count it as a mismatch, but rather assign a positive score! Otherwise, if we are below the threshold, then it just applies the same constant penalty. I thought this was cool and would've been surprised if no one had done it before. Turns out, someone has done it before, but I couldn't find anything from before 2020. Here is what some postdoc did last year: link. It's basically the same thing, but he uses a slightly different score function! Anyway, I was pleased with how this score function seemed to work in practice.
Combining Greediness and Optimality!

You're still here? Incredible. We are now going to do the (perhaps obvious) thing and simply combine Greedy Tiling and Smith-Waterman! In more detail, for each of the $k$ documents retrieved during source retrieval we do the following:
- Find all the exact matches of length at least $s$ words (I usually pick $s$ to be quite low, say 2 or 3) between the source document and the query document with Greedy Tiling.
- For each exact match found in the previous step, look at the $\ell$ words (I think $\ell = 50$ is a reasonable number to start off with, but it depends on the application) preceding and coming after the match in both the query and the source document, and run the Smith-Waterman on these $s + 2\ell$ words, considering only the top match in this range. If the score of the match according to Smith-Waterman is higher than some threshold $\beta$, then keep the match, otherwise discard it.

Note also that, by design, the Greedy Tiling phase catches proper nouns/names with at least 2-3 words, but if the surrounding context is unrelated in the source and query document then Smith-Waterman will recognize this and discard the match. I think that's pretty nice! Finally, I'll note that this combination of Greedy Tiling and Smith-Waterman was at least partially inspired by the (apparently famous) BLAST algorithm" from bioinformatics, which does something quite similar.
Finally, I'll note that this is just one way I thought was nice, efficient, and seemed to work well. There are doubtless many other text alignment texhniques you could go for, and a rather simple solution if you have a good exact match finder is to replace each word with a set of synonyms (and count two words as matching if they are in the same synonym set). One could also try and use some neural network approach that "understands" semantic similarities between two passages, but I have the feeling this would have a significantly slower runtime.
Now back to theory!