Crossing Numbers and a Sum-Product Theorem.

In this post I am gonna talk about some (sum) super fun stuff, with very slick proofs. Let $A \subseteq \mathbb R_+$ be a set with $n$ elements. Consider the "sum set" $$A + A := \{ a+b \: : \: a, b, \in A\}$$ and the "product set" $$A \cdot A := \{ a\cdot b \: : \: a, b, \in A\},$$ which is not to be confused with the cartesian product. It is easy to note that both of these, on their own, can be small. For example, if $A = \{1,...,n\}$ (or for that matter any arithmetic progression), then we have that $|A+A| =2n-1$. However, in this case, $|A\cdot A|$ is nearly (but not quite) $n^2$. On the other hand, when $A = \{ 1 ,2 ,4, ..., 2^n\}$ (or any other geometric progression), we have that $|A \cdot A| \leq 2n-1$, but that $A+A$ has nearly $n^2$ elements. Long ago, Erdös asked if this was a general phenomenon, i.e. if it was true that in general, for all $\epsilon > 0$, we have that $$T_A := \max \{ |A + A|, |A \cdot A|\} \geq n^{2-\epsilon}.$$ We haven't quite proved this yet, but we have made some very interesting progress over the years.

Agenda

In this post I will discuss a beautiful result of Elekes, who showed that $T_A \geq \Omega(n^{5/4})$. In order to give a self contained proof, we have to discuss some other interesting results and consequences related to crossing numbers of graphs, but trust me it will be worth it!

I will not be covering what is essentially the state-of-the-art which is a lovely proof from Solymosi that $T_A \geq \tilde \Omega (n^{4/3})$. There are two reasons for this:

Timothy Gowers already gave a great exposition of this result, and I don't want to reinvent the wheel here or even attempt to compete with Tim Gowers.
This post would become prohibitively long (not that Solymosi's proof is long -- it isn't!).

Crossing Numbers and Consequences

Let's completely switch gears for the moment. Given a graph $G$ with $n$ vertices and $m$ edges, we can attempt to draw it in the plane. The crossing number is the minimum number of times we must "cross" edges in order to do so. We say that a graph is "planar" if its crossing number is zero! (One of) Euler's Theorem(s) gives a famous way of relating the number of edges, faces, and vertices if the graph is planar:

If $G$ is planar, and $f$ is the number of faces in the planar drawing, then we have that $$n - m + f= 2.$$

It's a good exercise to show that the above theorem implies that $K_5$, the complete graph on 5 vertices, is not planar.

Here's another fun corollary that shows the power of this theorem.

If $m = 3n-5$, then $G$ is not planar.

Define the degree of a face $d(f)$ as the number of edges that surround it. It is easy to see that $\sum_f d(f) = 2m$. Moreover, we know that each face has to have degree at least 3. So, we have that $$2m = \sum_f d(f) \geq 3f.$$ Plugging this and the fact that $m = 3n -5$ into Euler's formula, we see that $$n -m + f \leq n - m + \frac{2}{3}m = n - \frac{1}{3}m = n - n + 5/3 < 2,$$ which contradicts Euler's theorem.

Ok, now lets get to some less TCS 101 intro stuff. What can we say in general about larger $m$? For the sake of not letting the length of this post get too out of hand, I'll just get right to it. Here's the lovely theorem.

Let $g(n,m)$ be the minimum crossing number of a graph with $n$ vertices and $m$ edges. Then, when $m \geq 4n$, we have that there exists constants $0< c_1,c_2 < 1$ such that $$c_1 \frac{m^3}{n^2} \leq g(n,m) \leq c_2 \frac{m^3}{n^2}.$$

The upper bound is easier because it is existential -- one must merely show the existence of such a graph. The basic idea is that we can take $\ell$ such that $n\ell \approx 2m$, and let $G$ be a graph with $n/\ell$ disjoint copies of $K_\ell$, each of which has crossing number $\Theta(\ell^4)$. I won't dwell on this here, for details see here. (Side note, if anyone can find a copy of the paper "A minimal problem concerning complete plane graphs" by Blažek and Koman, please send me an email. I spent half an hour with no dice.) The lower bound is more interesting, and its proofs can be attributed to Leighton and Ajtai, Chvátal, Newborn, and Szemerédi. The proof I present here is a slightly modified version of the latter.

let $cr(G)$ denote the crossing number of $G$.
First, we claim that $cr(G) \geq m - 3n + 6$. We can prove this via induction on $m$. If $m \leq 3n-6$ then the bound holds trivially. If $m > 3n-6$ then via the above corollary there must be at least one crossing. Delete one of the edges involved in this crossing, leaving a graph with $m-1$ edges. By the induction hypothesis, this graph has $m - 1 - 3n + 6$ crossings, establishing what we want.

Ok, now we claim that $cr(G) \geq \frac{1}{125} \frac{m^3}{n^2}$. This time, we shall induct on $n$. Note that, since $m \leq n(n-1)/2$, the first time it is possible for $m \geq 4n$ is when $n =9$, and in this case it must be that $m=36$ (i.e. we have a complete graph). In this case, a calculation shows that $cr(G) \geq m -3n + 6 =15 \geq \frac{36^3}{125\cdot 9^2}$. Alright then, that settles the base case. From now on $n \geq 10$.

Case 1: Suppose $4n \leq m \leq 5n$. In this case, we have that $$\frac{m^3}{125\cdot n^2} \leq n \leq m - 3n + 6 \leq cr(G),$$ so we are done.
Case 2: Now suppose $m > 5n$. Consider a single crossing $c$, which involves two edges. Now consider removing a vertex $v$ from the graph. The crossing $c$ remains in the subgraph $G-v$ (which is just $G$ without vertex $v$) iff $v$ was not involved in the crossing. Therefore, we can "overcount" each crossing $c$ at most $n-4$ times. Thus, $$cr(G) \geq \frac{1}{n-4}\sum_v cr(G - v).$$ We let $m_v$ denote the number of edges in $G-v$. Note then that $\sum_v m_v = (n-2) m$. Via Jensen's inequality, we also have that $$\sum_v m_v^3 = n \mathbb E [m_v^3] \geq n \mathbb E [m_v]^3 = n (m(n-2)/n)^3.$$ With this in mind and the fact that $m_v \geq 4(n-1)$, we can apply the induction hypothesis to $G-v$: \[ \begin{align*} cr(G) &\geq \frac{1}{n-4}\sum_v cr(G - v) \\ &\geq \frac{1}{n-4} \frac{1}{125\cdot (n-1)^2}\sum_v m_v^3 \\ &\geq \frac{1}{125}\frac{m^3 (n-2)^3}{n^2(n-1)^2 (n-4)} \end{align*} \] To finish the argument, it suffices to note that $(n-2)^3 = n^3 - 6n^2 + 12n -8$ and $(n-1)^2(n-4) = n^3 - 6n^2s + 9n - 4 \leq (n-2)^3$ for all $n \geq 10$.

This proof, while simpler to parse, is a slightly weaker than what was proved by Ajtai, Chvátal, Newborn, and Szemerédi (they get the constant $1/100$).

Using Crossing number Theorems to Achieve Ekeles' Bound

Ok, we are so close to proving Ekeles' bound! Just one more corollary!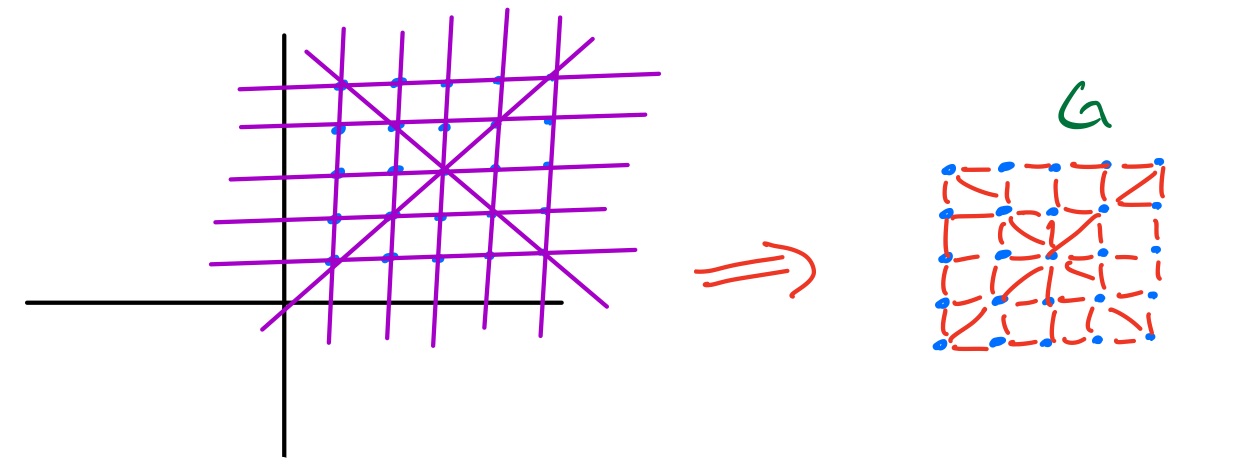

Suppose we have $n$ points in $\mathbb R^2$, the euclidean plane, and $\ell$ lines that pass through at least $k$ points, where $2 \leq k \leq \sqrt {n}$. Then we have the bound $\ell \leq O(n^2/k^3)$.

The above actually a relatively famous theorem originally due to Szemerédi and Trotter. Note that an upper bound of $O(n^2 /k^2)$ would be simple -- just consider the number of pairs of points each of the $\ell$ lines contains. The simple proof (one could even say from the book) I present next is due to Székely.

We are going to use the crossing number theorem we spent so much time proving in the previous section. So let's define a graph. Let $G$ be the graph that puts an edge between two of the points iff they are both next to each other on a line with at least $k$ points. See below example.

diagram converting plane with points and lines to graph — An example of converting $n \times n$ grid with lines to a graph. Note that this demonstrates the above corollary is tight, since here $k = \sqrt{n}$ and $\ell \geq \Omega(n^2/k^3)$. Note however in this example the crossing number is zero.

Note that each of the $\ell$ lines contains at least $k-1$ edges, none of which cross each other. Next, observe that $cr(G) \leq \ell^2$ trivially. Therefore, when $\ell (k-1) \geq 4n$, we can apply our crossing number theorem to obtain $$\ell^2 \geq cr(G) \geq \frac{(\ell(k-1))^3}{125\cdot n^2}.$$ Rearranging gives the bound. Otherwise, we have that $$\ell \leq \frac{4n}{k-1} \lesssim \frac{n}{k} = \frac{n^2}{nk} \leq n^2/k^3,$$ where we have used the fact that $2 \leq k \leq \sqrt n$.

Armed with this theorem, we can now prove Ekeles' result.

(Proof of Ekeles' bound $T \geq \Omega(n^{5/4})$)

For each $a_i, a_j \in A$, define $f_{ij}(x) = a_i(x - a_j)$. The key observation is that this function (which is notably linear), maps at least $n$ points from $A+A$ to $A\cdot A$. Indeed, plugging in $a_j + a_k$ for any $a_k$ results in $a_i\cdot a_k$. Let $P = (A + A)\times (A\cdot A)$ be our set of points, and note that $n \leq \sqrt{|P|}$. Note also that the number of lines with at least $n$ points is at least the number of functions we have defined, which is $n^2$. Then we can apply the above corollary to obtain that $$\ell = n^2 \lesssim \frac{|P|^2}{n^3}.$$ Rearranging gives $|P|^2 \geq n^5$, which implies that $T_A \geq n^{5/4}$, as desired!

← Previous Post